Frans van Schooten behandelde in zijn boek "Mathematische Oeffeningen" verschillende manieren om een lijn in twee gelijke stukken te delen. We gaan één van die manieren bekijken.
Van Schooten noemt het lijnstuk dat hij doormidden gaat delen AB.
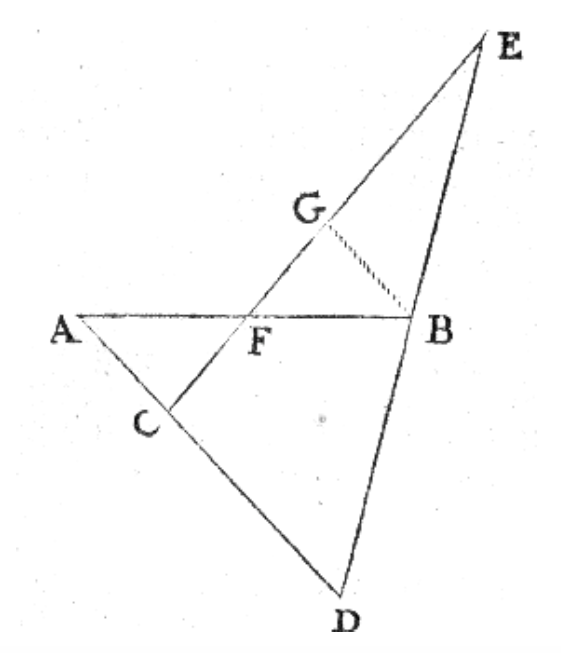
Op bladzijde 126 van het boek van Van Schooten staat te lezen hoe de punten A, B, C, D, E, F en G gekozen zijn. Er staat dat 2 × AC = CD en dat BD = BE. Punt G is het midden van CE; zie afbeelding.
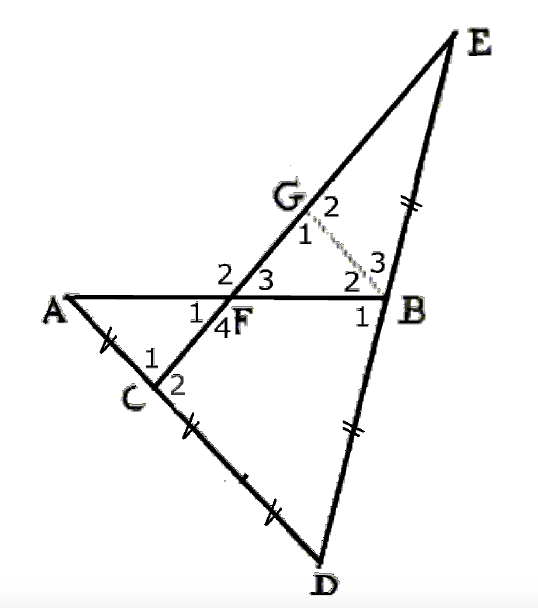
We gaan in stapjes aantonen dat F inderdaad het midden van AB is. In de volgende onderdelen kun je het werkblad gebruiken (zie 2de afbeelding)
a) Toon aan dat driehoek CDE gelijkvormig is met driehoek GBE. Wat is de
vergrotingsfactor?
b) Toon aan dat BG evenwijdig is aan DA.
c) Waarom geldt nu dat BG = AC?
d) Bewijs nu dat AF = BF.